Question

Andrew walks his sister to school every day. They walk 0.25 miles south, and then 0.25 miles west to get to school. Approximately how far are they from home if they could have walked diagonally across the park?

Answer 1

0.35355 miles

Explanation:

Because it is the "Correct Answer"

Answer 2

Approximately 0.35355 miles.

Explanation:

You find this by using the Pythagorean Theorem, which is
`a^2+b^2=c^2`. The Pythagorean Theorem finds the length of the hypotenuse, or the longest side of a triangle using the two shorter sides.

In this case, plug in .25 and .25 into A and B because they are the short sides of the triangle.

`.25^2+.25^2=c^2`

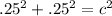
Now we have this.

`.25^2+.25^2=.125`

Next, solve for C.

`.125=c^2`

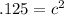
Square root both sides.

`√(.125)=√(c^2)`

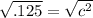
Simplify.

`.35355339059=c`

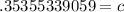
This answer makes sense because it is longer than the other two sides, but shorter than the two sides added together. Of course, walking diagonally from one point to another requires less distance than walking south then west to it.