Question

Find the mass of 3.27 x 10^23 molecules of H2SO4. Use 3 significant digits
and put the units.

Answer 1

Approximately
`53.3\; \rm g`.

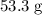Step-by-step explanation:

Lookup Avogadro's Number:
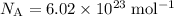`N_(\rm A) = 6.02* 10^(23)\; \rm mol^(-1)` (three significant figures.)

Lookup the relative atomic mass of
`\rm H`,
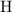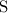`\rm S`, and
`\rm O` on a modern periodic table:

• 
  `\rm H`:
  `1.008`.
• 
  `\rm S`:
  `32.06`.
• 
  `\rm O`:
  `15.999`.

(For example, the relative atomic mass of
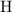`\rm H` is
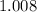`1.008` means that the mass of one mole of
`\rm H\!` atoms would be approximately
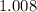`1.008\!` grams on average.)

The question counted the number of
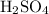`\rm H_2SO_4` molecules without using any unit. Avogadro's Number
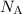`N_(\rm A)` helps convert the unit of that count to moles.

Each mole of
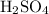`\rm H_2SO_4` molecules includes exactly
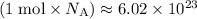`(1\; {\rm mol} * N_\text{A}) \approx 6.02* 10^(23)` of these
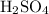`\rm H_2SO_4 \!` molecules.

`3.27 * 10^(23)`
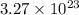
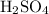`\rm H_2SO_4` molecules would correspond to
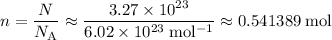`\displaystyle n = (N)/(N_(\rm A)) \approx (3.27 * 10^(23))/(6.02 * 10^(23)\; \rm mol^(-1)) \approx 0.541389\; \rm mol` of such molecules.

(Keep more significant figures than required during intermediary steps.)

The formula mass of
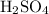`\rm H_2SO_4` gives the mass of each mole of
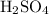`\rm H_2SO_4\!` molecules. The value of the formula mass could be calculated using the relative atomic mass of each element:

`\begin{aligned}& M({\rm H_2SO_4}) \\ &= (2 * 1.008 + 32.06 + 4 * 15.999)\; \rm g \cdot mol^(-1) \\ &= 98.702\; \rm g \cdot mol^(-1)\end{aligned}`.

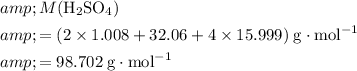Calculate the mass of approximately
`0.541389\; \rm mol` of
`\rm H_2SO_4`:

`\begin{aligned}m &= n \cdot M \\ &\approx 0.541389\; \rm mol * 98.702\; \rm g \cdot mol^(-1)\\ &\approx 53.3\; \rm g\end{aligned}`.

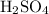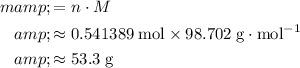(Rounded to three significant figures.)