Question

Please help me with this function on a closed interval!

Answer 1

(E) 13

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Equality Properties

• Multiplication Property of Equality
• Division Property of Equality
• Addition Property of Equality
• Subtraction Property of Equality

Algebra I

• Functions
• Function Notation

Calculus

Antiderivatives - Integrals

Integration Rule [Fundamental Theorem of Calculus 1]:
`\displaystyle \int\limits^b_a {f(x)} \, dx = F(b) - F(a)`

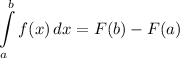
Integration Rule [Fundamental Theorem of Calculus 2]:
`\displaystyle (d)/(dx)[\int\limits^x_a {f(t)} \, dt] = f(x)`

Explanation:

Step 1: Define

`\displaystyle \int\limits^4_0 {f'(t)} \, dt = 8`

`\displaystyle f(4) = \text{unknown}`

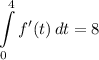
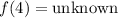
Step 2: Integrate

1. [Integral] Evaluate [Integration Rule - FTC 1 and 2]:
   `\displaystyle \int\limits^4_0 {f'(t)} \, dt = f(4) - f(0)`
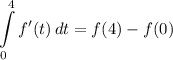
2. [Integral] Substitute in variables [Given/Table]:
   `\displaystyle 8 = f(4) - 5`
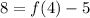
3. [Addition Property of Equality] Isolate f(4):
   `\displaystyle 13 = f(4)`
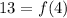
4. Rewrite:
   `\displaystyle f(4) = 13`

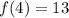
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Integration

Book: College Calculus 10e