Question

Line segment AB on the coordinate plane stretches from (1,1) to (7,9). Line segment CD stretches from (-2,3) to (2,6). What is the ratio AB:CD of the lengths of these line segments

A. 3:2
B 2:1
C 2:3
D 3:1

Answer 1

B 2:1

Explanation:

Distance between two points:

Suppose that we have two points,
`(x_1,y_1)` and
`(x_2,y_2)`. The distance between them is given by:

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

In this question:

The length of the segments are given by the distance between its endpoints.

Line segment AB on the coordinate plane stretches from (1,1) to (7,9).

So its length is:

`√((7-1)^2+(9-1)^2) = √(6^2+8^2) = √(100) = 10`

Line segment CD stretches from (-2,3) to (2,6).

`√((2-(-2))^2+(6-3)^2) = √(4^2+3^2) = √(25) = 5`

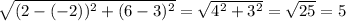
What is the ratio AB:CD of the lengths of these line segments?

10:5 = 2:1

So the correct answer is given by option B.