Question

The verticals of the triangle shape are A (-2, 4) , B (-2,3) , and C (-5,2). If ABC is reflected across the line y = -1 to produce the image of A'B'C', What's the coordinate of B' after a reflection across the line y=-1?

​

Answer 1

Given:

The vertices of a triangle are A (-2, 4) , B (-2,3) , and C (-5,2).

Triangle ABC is reflected across the line y = -1 to produce the image of A'B'C'.

To find:

The coordinate of B' after a reflection across the line y=-1.

Solution:

If a figure is reflected across the line y=b, then

`(x,y)\to (x,-(y-b)+b)`

`(x,y)\to (x,-y+b+b)`

`(x,y)\to (x,2b-y)`

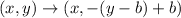
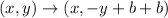
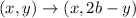
The given triangle ABC is reflected across the line y=-1. So, the rule of reflection is

`(x,y)\to (x,2(-1)-y)`

`(x,y)\to (x,-2-y)`

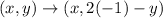
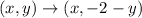
The coordinates of point B are (-2,3). So,

`B(-2,3)\to B'(-2,-2-3)`

`B(-2,3)\to B'(-2,-5)`

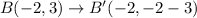
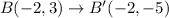
Therefore, the coordinates of point B' are (-2,-5).