Question

6. The number of bacteria N in a culture is given by the model N(t) = 250e 0.0156 where t is the time in hours.

Find how many hours it takes for the original population to double. Round your answer to the nearest hundredth
of an hour.

i just need to know how to work this out!! please help

Answer 1

t ≈ 44.43 hours

Explanation:

Expression that models the population of a bacteria after time 't' is,

N(t) =
`250(e^(0.0156t))`

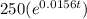
Here initial population = 250

And N(t) = Population after 't' hours

t = duration

We have to find the duration in which bacterial population gets doubled.

N(t) = 2×250 = 500

From the given expression,

500 =
`250(e^(0.0156t))`

`e^(0.0156t)=2`

`\text{ln}(e^(0.0156t))=\text{ln}(2)`

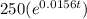
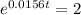
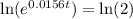
0.0156t[ln(e)] = 0.693147

0.0156t = 0.693147

t =
`(0.693147)/(0.0156)`

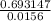
t = 44.432

t ≈ 44.43 hours