1 Answer

David Siegel · Answer 1 · 2022-01-25T02:05:51+0000

We are given with information that , we have to find two consecutive positive integers , sum of whose squares is 365 .

${\pmb{\bf Assumption \: :-}}$ Let's assume that the first number is x , and as the other no. is it's consecutive so , the second no. is (x+1)

Now , According to the question ;

${: \implies \quad \sf x^(2)+x^(2)+1^(2)+ 2\cdot x \cdot 1 = 365\quad \{\because (a+b)^(2)=a^(2)+b^(2)+2ab\}}$

Can be further written as ;

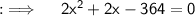
${: \implies \quad \sf 2{x^(2)}+2x -364=0}$

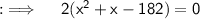
${: \implies \quad \sf 2(x^(2)+x-182)=0}$

As ,
$\sf 2 \\eq 0$ . So ;

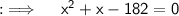
${: \implies \quad \sf x^(2)+x-182=0}$

Using splitting the middle term ;

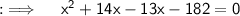
${: \implies \quad \sf x^(2) +14x-13x-182=0}$

${: \implies \quad \sf x(x+14)-13(x+14)=0}$

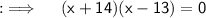
${: \implies \quad \sf (x+14)(x-13)=0}$

When (x+14) = 0 , then x = - 14 , which is rejected as it's not +ve

When (x-13) = 0 , then x = 13 , which is +ve

Now ,

Hence , The required numbers are 13 and 14 respectively .

Please log in or register to add a comment.