We are given –
- Height (h) of cone is = 19.9cm
- Radius (r) of cone is = 9.6 cm
According to the question, we are asked to find out volume of the cone. As we know –
Substituting values –

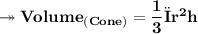

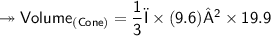

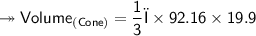

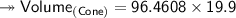

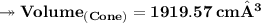

Know More –
- C.S.A of cone = πrl
- T.S.A of cone = πrl + πr²
- Volume of cuboid = l × b × h
- C.S.A of cuboid = 2(l + b)h
- T.S.A of cuboid = 2(lb + bh + lh)
- C.S.A of cube = 4a²
- T.S.A of cube = 6a²
- Volume of cube = a³
- Volume of sphere = 4/3πr³
- Surface area of sphere = 4πr²
- Volume of hemisphere = ⅔ πr³
- C.S.A of hemisphere = 2πr²
- T.S.A of hemisphere = 3πr²
_________________________________________