Question

Given the triangle below, find the angle θ in radians. Round to four decimal places.

Answer 1

theta = 0.9626 radians

Explanation:

cos theta = a/h

cos theta = 4/7 = 0.5714

so, the angle theta = arc cos 0.5714 =

55.1520 °

in radians => 55.1520 × π / 180°

= 0.9626 radians

Answer 2

θ = 0.9626

Explanation:

Hi there!

We're given the hypotenuse and the leg adjacent to θ in this right triangle. To find θ, we can use the cosine ratio:

`\displaystyle cos\theta=(adjacent)/(hypotenuse)`

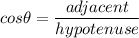
Plug in the given information

`\displaystyle cos\theta=(4)/(7)`

Use the inverse cosine ratio

`\displaystyle \theta=cos^-^1((4)/(7))`

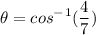
Plug this into your calculator (and ensure you're solving for radians instead of degrees in the settings)

`\displaystyle \theta=0.9626`

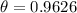
Therefore, θ = 0.9626 when rounded to four decimal places.

I hope this helps!