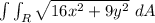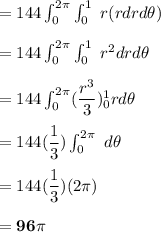Question

The transformation x=au, y=bv (a>0, b>0) can be rewritten as x/a=u, y/b=v, and hence it maps the curricular region u2+v2≤1 into the elliptical region x2/a2+y2/b2≤1. In these exercises, perform the integration by transforming the elliptical region of integration into a circular region of integration and then evaluating the transformed integral in polar coordinates.

∬R16x2+9y2dA

,where R is the region enclosed by the ellipse

(x2/9)+(y2/16)=1

Answer 1

96π

Explanation:

The transformation x = au , y = bv (a>0, b>0) can be re-written as;

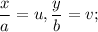`(x)/(a)= u , (y)/(b)=v ;` which maps the circular region u² + v² ≤ 1 into the elliptical region

`(x^2)/(a^2)+(y^2)/(b^2)\le 1`

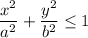
Integrating and transforming the elliptical region into a circular region;

`\int \int _R √(16x^2+9y^2)\ dA`

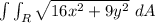
here;

R = region enclosed by the ellipse.

`(x^2)/(9)+(y^2)/(16)=1`

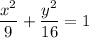
Let x = 3u ; y = 4v

Jocobian = J(x,y)

`= \left[\begin{array}{ccc}(\partial x)/(\partial u)&(\partial x)/(\partial v)\\(\partial y)/(\partial u)&(\partial y)/(\partial v)\\\end{array}\right] \\ \\ \\ \\ = \left[\begin{array}{ccc}3&0\\0&4\\\end{array}\right] \\ \\ \\ = 12`

So;

`\int \int_R √(16x^2+9y^2 \ dA)= \int \int _D√(16(4u)^2+9(3v)^2) \ |J| dudv \\ \\ \\= 12 \int \int _D √(x^2 +v^2) \ \ (12) dudv \\ \\ \\ =144 \int \int _D √(x^2 +v^2) \ \ dudv`

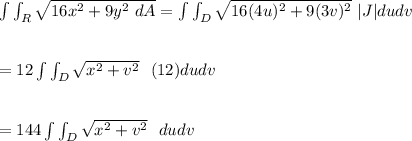
Using polar coordinates;

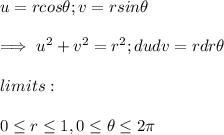
`u = rcos \theta ; v = rsin \theta \\ \\ \implies u^2+v^2 = r^2 ; dudv = rdr \theta \\ \\ limits :\\ \\ 0 \le r \le 1, 0\le \theta \le 2 \pi`

∴

`\int \int _R √(16x^2 + 9y^2 )\ dA`

`= 144 \int ^(2 \pi)_(0) \int ^(1)_(0) \ r (rdrd \theta) \\ \\ = 144 \int ^(2 \pi)_(0) \int ^(1)_(0) \ r^2drd \theta \\ \\ = 144 \int ^(2 \pi)_(0)((r^3)/(3))^1_0 r d \theta \\ \\ = 144 ( (1)/(3)) \int ^(2 \pi)_(0) \ d \theta \\ \\ = 144((1)/(3)) ( 2 \pi) \\ \\ \mathbf{= 96 \pi}`