Question

In manufacturing a particular set of motor shafts, only shaft diameters of between 38.20 and 37.50 mm are usable. If the process mean is found to be 37.80 mm with a standard deviation of 0.20 mm, what percentage of the population of manufactured shafts are usable?

Answer 1

we can conclude that 91.04% population of shafts are usable

Step-by-step explanation:

Given that;

X
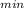`_(min)` = 37.50 mm

X
`_(max)` = 38.20 mm

mean μ = 37.80

standard deviation σ = 0.20 mm

This problem is based on normal probability distribution so, to get the probability, we must calculate; z = x-μ / σ

so;

Z
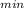`_(min)` = (X
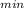`_(min)` - μ) / μ = (37.50 - 37.80) / 0.20 = -1.5

Z
`_(max)` = (X
`_(max)` - μ) / μ = (38.20 - 37.80) / 0.20 = 2

Hence;

P( 37.50 < X < 38.20 ) = P( -1.5 < Z < 2 )

P( 37.50 < X < 38.20 ) = P( 0 < Z < 1.5 ) + P( 0 < Z < 2 )

from the standard normal table table;

P( 37.50 < X < 38.20 ) = 0.4332 + 0.4772

P( 37.50 < X < 38.20 ) = 0.9104 = 91.40%

Hence, we can conclude that 91.04% population of shafts are usable