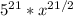Final Answer:
The quantity
![[(5√(x) )^7]^3](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/s7opj9n2ry6ru1tjt5k2.png) can be transformed into an expression with a rational exponent by applying the properties of exponents and simplifying the radicals:
can be transformed into an expression with a rational exponent by applying the properties of exponents and simplifying the radicals:
![[(5√(x) )^7]^3 = (5^7)(x^((7/2)))^3 = 5^21 * x^((21/2))](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/gbrbyh1n79s5mit8c5r4.png)
Step-by-step explanation:
Apply the power of a power rule: We can start by breaking down the expression inside the parentheses:
![[(5√(x) )^7]^3 = (5^((7/2)))^3](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/wzucfae9upa8uv7m4ae9.png)
Simplify the radicals: Since we have a power of another power, we can simplify the radical:
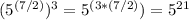
Combine exponents with the same base: Now we can combine the exponents with the same base:
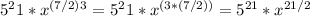
Therefore, the transformed expression with a rational exponent is