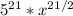Question

Describe how to transform the quantity of the fifth root of x to the seventh power, to the third power into an expression with a rational exponent.
`(5√(x) ^7)^3`

Answer 1

unnun

Step-by-step explanation:

Answer 2

The quantity
`[(5√(x) )^7]^3` can be transformed into an expression with a rational exponent by applying the properties of exponents and simplifying the radicals:

`[(5√(x) )^7]^3 = (5^7)(x^((7/2)))^3 = 5^21 * x^((21/2))`

Step-by-step explanation:

Apply the power of a power rule: We can start by breaking down the expression inside the parentheses:

`[(5√(x) )^7]^3 = (5^((7/2)))^3`

Simplify the radicals: Since we have a power of another power, we can simplify the radical:

`(5^((7/2)))^3 = 5^((3 * (7/2))) = 5^(21)`

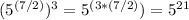
Combine exponents with the same base: Now we can combine the exponents with the same base:

`5^21 * x^((7/2))^3 = 5^21 * x^((3 * (7/2))) = 5^(21) * x^(21/2)`

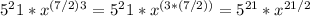
Therefore, the transformed expression with a rational exponent is
`5^(21) * x^(21/2)`