Question

`Find \: H.C.F \: of \: \\ 900 \: , 270 \\ using \: e.d.l \: \\ ( \: Euclid's \: division \: lemma \: )`

H.C.F of 900 & 270 ​

Answer 1

• 90

Explanation:

Factorize both numbers:

• 900 = 2*2*3*3*5*5
• 270 = 2*3*3*3*5

Common factors are:

• 2*3*3*5

So HCF is:

• HCF(900, 270) = 2*3*3*5 = 90

Answer 2

See Above Attachment ⇡

`\Large \red \mid \: \underline {\rm {{{\color{blue}{Explanation...}}}}} \: \red \mid`

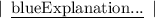
We know that ,

As per Euclid Division Algorithm.

`\longrightarrow \: \Large\underbrace {\rm {{{\color{red}{ \: a \: = \: bq \: + \: r \: }}}}}`

• a denotes dividend

• b denotes divisor

• q denotes quotient

• r denotes remainder

◆━━━━━▣✦▣━━━━━◆

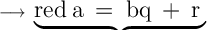
Using Euclid Division Algorithm

`\large\bf{\purple{ \hookrightarrow \: }} \tt \: \: 900 \: = \: 270 \: * \: 3 \: + \: 90`

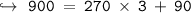
Here ,

`\large\bf{\orange{ \implies \: }} \: \:r \: \\eq \: 0`

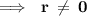
Again Applying Euclid Division Algorithm

`\large\bf{\purple{ \hookrightarrow \: }} \tt \: 270 \: = \: 90 \: * \: 3 \: + \: 0`

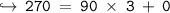
Here ,

`\large\bf{\orange{ \implies \: }} \: \:r \: = \: 0`

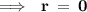
As the reminder is 0 , 90 will be the greatest common divisor for the two given numbers.

So,

`{\boxed{ \Large{ \blue{ \bf{ \underline{ HCF \: = \: 90}}}}}}`

◆━━━━━▣✦▣━━━━━◆