Question

Given f(x)=2x^3+kx-9f(x)=2x 3 +kx−9, and the remainder when f(x) is divided by x−2 is 23, then what is the value of k?

Answer 1

Given:

The function is

`f(x)=2x^3+kx-9`

The remainder when f(x) is divided by x−2 is 23.

To find:

The value of k.

Solution:

According to the remainder theorem, if a polynomial P(x) is divided by (x-c), then the remainder is P(c).

It is given that, the remainder when f(x) is divided by x−2 is 23. By using remainder theorem, we get

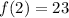`f(2)=23` ...(i)

Put x=2, to find the value of f(2).

`f(2)=2(2)^3+k(2)-9`

`f(2)=2(8)+2k-9`

`f(2)=16+2k-9`

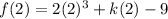
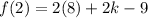
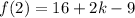
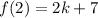`f(2)=2k+7` ...(ii)

Using (i) and (ii), we get

`2k+7=23`

`2k=23-7`

`k=(16)/(2)`

`k=8`

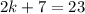
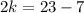
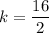
Therefore, the value of k is 8.