Question

A baker is building a rectangular solid box from cardboard to be able to safely deliver a birthday cake. The baker wants the volume of the delivery box to be 224 cubic inches. If the width of the delivery box is 3 inches longer than the length and the height is 4 inches longer than the length, what must the length of the delivery box be?

3 inches
7 inches
8 inches
4 inches

Answer 1

4 inches

Explanation:

just took test

Answer 2

4 inches.

Explanation:

Let l = length, w = width, and h = height

The formula for the volume of a rectangular solid would be V = lwh. We are tasked with finding the length of the delivery box. In order to find the length, we need to change the variables so that l is the only variable in the equation.

The prompt tells us that the width of the box is 3 inches longer than the length. That means that w = l + 3. Likewise, the prompt also informs us that the height is 4 inches longer than the length. Therefore, h = l + 4.

Now that the variables have been changed so that l is the only variable, we can finally solve for l.

`V=lwh\\\\224=l(l+3)(l+4)\\\\224=l^3+7l^2+12l\\\\0=l^3+7l^2+12l-224\\\\0=(l-4)(l^2+11l+56)`

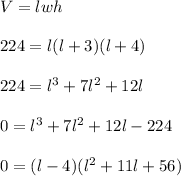
After factoring, we are left with (l - 4)(l² + 11l + 56) = 0. Ultimately, by using the quadratic formula, l² + 11l + 56 = 0 will have imaginary number solutions. However, l - 4 = 0 gives us l = 4. Therefore, the length of the delivery box is 4 inches.