Answer:
solution given:
(A) x^2 + 6x + 9 = 0
doing middle term
x^2+ (3+3)x+9=0
x^2 +3x+3x +9=0
taking common from two each term.
x(x+3)+3(x+3)=0
(x+3)(x+3)=0
either
x+3=0
x=-3
(B) 8x^2+ 5x - 6 = 0
Comparing above equation with
ax^2+bx+c=0,
we get,
a=8
b=5
c=-6
now
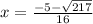
we have
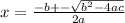
now substituting value:
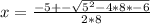
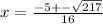
taking positive
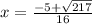
taking negative
(C) (x + 4)^2 - 36 = 0
(x + 4)^2 - 6^2 = 0
it is in the form of x²+y²:(x+y)(x-y)
so (x + 4)^2 - 6^2 can be written as (x+4+6)(x+4-6)
above equation becomes
(x+10)(x-2)=0
either
x=-10
or
x=2
Explanation: