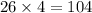Question

In the rhombus shown above, AC = 20 and DB = 48. Find the perimeter of the rhombus.

Answer 1

104

Explanation:

A rhombus diagonal bisect each other so that means half of the diagonal is equal to the other half.

Applying that, this means

• AE=EC
• DE=EB

Since they are equal we can divide AC by 2 to find AE and EC.

20/2=10

AE=10, EC=10

Same for DB

48/2=24

DE=24, EB=24

A rhombus diagonals are perpendicular to each other so each middle angle will measure 90 degree.

Looking closer, a rhombus has 4 right triangles. We only need to use one.

Look at triangle AEB. We know AE=10 and EB=24 and Angle E=90. We can apply pythagorean theorem to find side AB.

`{ae}^(2) + {db}^(2) = {ab}^(2)`

`{10}^(2) + {24}^(2) = {ab}^(2)`

`100 + 576 = ab {}^(2)`

`676 = {ab}^(2)`

`√(676) = 26`

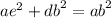
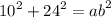
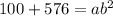
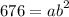
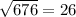
The perimeter of rhombus is equal to

4a, where a is the length of one side.

One side measures 26 so we can plug that in.

`26 * 4 = 104`