Question

Two mechanics worked on the car the first mechanic work for five hours in a sec mechanic work for 15 hours together the tires a total of 1850 what was the rate charge per hour about each mechanic if the sum of the two rates were $160 per hour

Answer 1

Mechanic 1: $55 per hour

Mechanic 2: $105 per hour

Explanation:

Given

Represent the rate of the first mechanic with x and the second with y.

So, we have:

`x + y = 160`

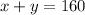
The total earnings is: $1850, so we have:

`5x + 15y = 1850`

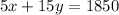
Required

Determine the rate of each

The equations are:

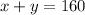`x + y = 160` --- (1)

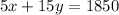`5x + 15y = 1850` --- (2)

Divide (2) through by 5

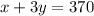`x + 3y = 370` --- (3)

Subtract (1) from (3)

`x - x + 3y - y = 370 - 160`

`2y = 210`

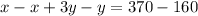
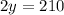
Divide through by 2

`y = (210)/(2)`

`y = 105`

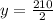
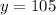
Substitute 105 for y in (1)

`x + y = 160`

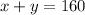
Make x the subject

`x = 160 - y`

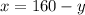
Substitute 105 for y

`x = 160 - 105`

`x = 55`

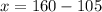
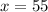
Hence:

Mechanic 1: $55 per hour

Mechanic 2: $105 per hour