Answer:
See Explanation
Explanation:
The question is incomplete. I will assume the function is:
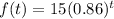
Required
Determine the rate of decay
In an exponential function
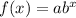 ,
,
The decay rate of the function is calculated as:

By comparison:

So, the equation becomes:
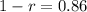
Make r the subject


The rate of decay is 0.14