Question

I need help with number 4

Answer 1

D

Step-by-step explanation:

let y = f(x) and rearrange making x the subject

y =
`√(x-2)` + 3 ( subtract 3 from both sides )

y - 3 =
`√(x-2)` ( square both sides )

(y - 3)² = x - 2 ( add 2 to both sides )

(y - 3)² + 2 = x

Change y back into terms of x with x =
`f^(-1)` (x) , then

`f^(-1)` (x) = (x - 3)² + 2 → D

Answer 2

Answer: Choice D

`f^(-1)(x) = (x-3)^2+2\\\\`

============================================================

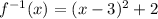
Step-by-step explanation:

First we replace f(x) with y. This is because both y and f(x) are outputs of a function.

To find the inverse, we swap x and y and solve for y like so

`y = √(x-2)+3\\\\x = √(y-2)+3 \ \text{ .... swap x and y; isolate y}\\\\x-3 = √(y-2)\\\\(x-3)^2 = y-2 \ \text{ ... square both sides}\\\\(x-3)^2+2 = y\\\\y = (x-3)^2+2\\\\f^(-1)(x) = (x-3)^2+2\\\\`

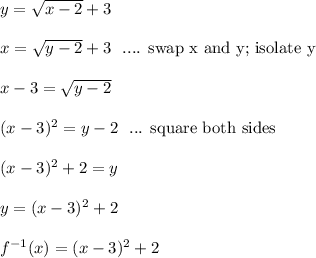
Note: because the range of the original function is
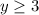`y \ge 3`, this means the domain of the inverse is
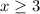`x \ge 3`. The domain and range swap roles because of the swap of x and y.

As the graph shows below, the original and its inverse are symmetrical about the mirror line y = x. One curve is the mirror image of the other over this dashed line.