Question

A cylindrical bar of metal having a diameter of 20.5 mm and a length of 201 mm is deformed elastically in tension with a force of 46300 N. Given that the elastic modulus and Poisson's ratio of the metal are 60.5 GPa and 0.33, respectively, determine the following: (a) The amount by which this specimen will elongate in the direction of the applied stress. (b) The change in diameter of the specimen. Indicate an increase in diameter with a positive number and a decrease with a negative number.

Answer 1

a) The amount by which this specimen will elongate in the direction of the applied stress is 0.466 mm

b) The change in diameter of the specimen is - 0.015 mm

Explanation:

Given the data in the question;

(a) The amount by which this specimen will elongate in the direction of the applied stress.

First we find the area of the cross section of the specimen

A =
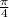`(\pi )/(4)` d²

our given diameter is 20.5 mm so we substitute

A =
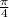`(\pi )/(4)` ( 20.5 mm )²

A = 330.06 mm²

Next, we find the change in length of the specimen using young's modulus formula

E = σ/∈

E = P/A × L/ΔL

ΔL = PL/AE

P is force ( 46300 N), L is length ( 201 mm ), A is area ( 330.06 mm² ) and E is elastic modulus (60.5 GPa) = 60.5 × 10⁹ N/m² = 60500 N/mm²

so we substitute

ΔL = (46300 N × 201 mm) / ( 330.06 mm² × 60500 N/mm² )

ΔL = 0.466 mm

Therefore, The amount by which this specimen will elongate in the direction of the applied stress is 0.466 mm

(b) The change in diameter of the specimen. Indicate an increase in diameter with a positive number and a decrease with a negative number.

Using the following relation for Poisson ratio

μ = - Δd/d / ΔL/L

given that Poisson's ratio of the metal is 0.33

so we substitute

0.33 = - Δd/20.5 / 0.466/201

0.33 = - Δd201 / 20.5 × 0.466

0.33 = - Δd201 / 9.143

0.33 × 9.143 = - Δd201

3.01719 = -Δd201

Δd = 3.01719 / - 201

Δd = - 0.015 mm

Therefore, The change in diameter of the specimen is - 0.015 mm