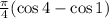Question

Evaluate the given integral by changing to polar coordinates.

∫ ∫ sin(x2 + y2) dA
R

where R is the region in the first quadrant between the circles with center the origin and radii 1 and 2

Answer 1

The result of the integral is
`(\pi)/(4)(cos(4)-cos(1))`

Explanation:

Polar coordinates:

In polar coordinates, we have that:

`r^2 = x^2 + y^2`

`\int \int_(R) dA = \int \int_(R) r dr d\theta`

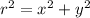
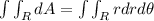
In which r is related to the radius values, while
`\theta` is related to the angles in the trigonometric circle.

In this question:

R is the region in the first quadrant

In the first quadrant in the trigonometric circles, the angles go from 0 to
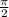`(\pi)/(2)`, which means that this are the outer limits of integration.

Between the circles with center the origin and radii 1 and 2

This means that the inner limits of integration are between 1 and 2.

The integral will be given by:

`\int \int_(R) \sin{x^2+y^(2)} dA = \int_(0)^{(\pi)/(2)} \int_(1)^(2) sin(r^2) r dr d\theta`

Inner integral:

`\int_(1)^(2) sin((r^2)) r dr`

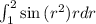
By substituion,

`u = r^2`

`du = 2r dr`

`dr = (du)/(2r)`

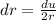
So

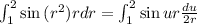`\int_(1)^(2) sin((r^2)) r dr = \int_(1)^(2) sin(u) r (du)/(2r)` = \frac{1}{2} \int_{1}^{2} \sin{u} du[/tex]

Integral of sine is minus cosine. So

`(1)/(2)(cos(u))|_(1)^(2)`

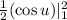
Before replacing, we substitute back u.

`(1)/(2)(cos(r^2))|_(1)^(2) = (1)/(2)(cos(4)-cos(1))`

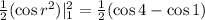
Outer integral:

`\int_(0)^{(\pi)/(2)} (1)/(2)(cos(4)-cos(1)) d\theta`

`(\theta)/(2)(cos(4)-cos(1))_(0)^{(\pi)/(2)}`

`(\pi)/(4)(cos(4)-cos(1))`

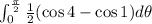
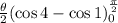
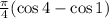
The result of the integral is
`(\pi)/(4)(cos(4)-cos(1))`