Question

Round 1 of a tennis tournament starts with 64 players. After each round, half of the players have lost and are eliminated from the tournament. Therefore, in round 2 there are 32 and in round 3 there are 16 players and so on. Can this relationship be modeled by a linear function? Provide evidence to support your claim.

Answer 1

It can not be modeled by a linear function

Explanation:

The given parameters can be represented as:

`(x_1,y_1) = (1,64)`

`(x_2,y_2) = (2,32)`

`(x_3,y_3) = (3,16)`

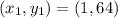
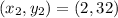
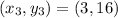
Where: x = rounds and y = players

Required:

Determine if it can be represented by a linear function

To do this, we simply calculate the slope (m)

`m = (y_2 - y_1)/(x_2 - x_1)`

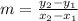
and

`m = (y_3 - y_2)/(x_3 - x_2)`

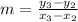
Using:
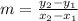`m = (y_2 - y_1)/(x_2 - x_1)`, we have:

`m = (32 - 64)/(2 - 1)`

`m = (-32)/( 1)`

`m = -32`

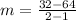
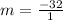
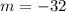
Using
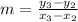`m = (y_3 - y_2)/(x_3 - x_2)`, we have:

`m = (16 - 32)/(3 - 2)`

`m = (-16)/(1)`

`m = -16`

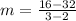
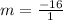
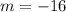
Since both slopes are not the same, the relationship be modeled by a linear function