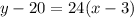Question

Find an equation of the tangent line to the curve at the given point. y = x3 − 3x + 2, (3, 20)

Answer 1

`y - 20 = 24(x - 3)`

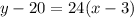
Explanation:

Equation of a line:

The equation of a line, in point-slope form, has the following format:

`y - y_0 = m(x - x_0)`

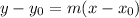
In which the point is
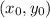`(x_0,y_0)` and the slope is m.

(3, 20)

This means that
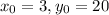`x_0 = 3, y_0 = 20`. So

`y - y_0 = m(x - x_0)`

`y - 20 = m(x - 3)`

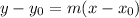
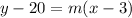
Slope:

The slope is the derivative of the function at the point:

The function is:

`y = x^3 - 3x + 2`

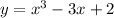
The derivative is:

`y^(\prime)(x) = 3x^2 - 3`

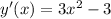
At the point, we have that
`x = 3`. So

`m = y^(\prime)(3) = 3*3^2 - 3 = 27 - 3 = 24`

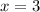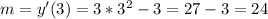
So the equation to the tangent line to the curve a the point is:

`y - 20 = 24(x - 3)`