Graph 1
Part (a)
The function is increasing when x > 0. The function is decreasing when x < 0.
The function is never constant
An increasing portion is when the graph goes uphill when moving left to right. A decreasing portion goes in the opposite direction: it goes downhill when moving left to right.
The reason why the function is never constant is because there aren't any flat horizontal sections. Such sections are when x changes but y does not. No such sections occur.
------------------------
Graph 1
Part (b)
Domain = set of all real numbers
Range = set of y values such that
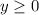
The domain is the set of all real numbers because we can plug in any value for x without any restriction. There are no division by zero errors to worry about, or square roots of negative numbers to worry about either.
The range is the set of nonnegative numbers as the graph indicates. The lowest y gets is y = 0.
------------------------
Graph 1
Part (c)
The function is even
The function f(x) = 1.6x^12 is an even function due to the even number exponent. For any polynomial, as long as the exponents are all even, then the function itself is even. If all the exponents were odd, then the function would be odd. This applies to polynomials only. A power function is a specific type of polynomial.
Note in the graph, we have y axis symmetry. The mirror line is vertical and placed along the y axis. This is a visual trait of any even function.
We could use algebra to show that f(-x) = f(x) like so
f(x) = 1.6x^12
f(-x) = 1.6(-x)^12
f(-x) = 1.6x^12
The third step is possible because (-x)^12 = x^12 for all real numbers x. It's similar to how (-x)^2 = x^2. You could think of it like (-1)^2 = (1)^2
============================================================
Graph 2
Part (a)
The function is decreasing when x < 0 and when x > 0
The function is never increasing
The function is never constant
In other words, the function is decreasing over the entire domain (see part b). The only time it's not decreasing is when x = 0.
The function is decreasing because the curve is going downhill when moving to the right. You can think of it like a roller coaster of sorts.
At no point of this curve goes uphill when moving to the right. Therefore, it is never increasing. The same idea applies to flat horizontal sections, so there are no constant intervals either.
------------------------
Graph 2
Part (b)
Domain: x is any real number but
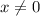
Range: y is any real number but
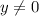
Explanation: If we tried plugging x = 0 into the function, we get a division by zero error. This doesn't happen with any other number. Therefore, the set of allowed inputs is any number but 0.
The range is a similar story. There's no way to get y = 0 as an output.
If we plugged y = 0 into the equation, then we'd get this
y = 17x^(-3)
0 = 17/(x^3)
There's no way to have the right hand side turn into 0. The numerator is 17 and won't change. Only the denominator changes. We can't have the denominator be 0.
------------------------
Graph 2
Part (c)
The function is odd
We can prove this by showing that f(-x) = -f(x)
f(x) = 17x^(-3)
f(-x) = 17(-x)^(-3)
f(-x) = 17* ( -(x)^(-3) )
f(-x) = -17x^(-3)
f(-x) = -f(x)
This is true for nearly all real numbers x, except we can't have x = 0.