Question

A wheel of radius 25cm has eight spokes. It is mounted on a fixed axle and is rotating at a constant angular speed w. You shoot a 20cm long arrow parallel to the axle through the wheel at a speed of 6m/s. The arrow and the spokes are supposed to be thin. Calculate the maximum value of w ( in rad/second and in rev/second) so that the arrow just goes through without hitting any of the spokes. Does it matter where between the axle and the rim of the wheel you aim? If so, what is the best location?

Answer 1

Answer:omega=23.56... rad/s

Explanation:for the arrow to pass without hitting the 8 spokes

taking the spokes thickness to be a point along the spokes linear motion path

lets calculate the time athe arrow pass point length of the wire 0.25m and it's speed(6m/s)

t=0.25m÷6m/s=0.0333...s

so every spoke around the wheel must move replacing each other's position so distribution of eight spokes=2π÷8=0.78... rad so using as angular displacement and t=0.033s then omega=∅/t=0.78/0.033=23.56rad/s

*yes

*space between spokes

Answer 2

Step-by-step explanation:

We will assume that the rim of the wheel is also very thin, like the spokes. The distance s between the spokes along the rim is

`s = (1)/(8)C = (1)/(8)(2\pi)(0.25\:\text{m}) = 0.196\:\text{m}`

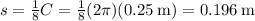
The 20-cm arrow, traveling at 6 m/s, will travel its length in

`t = \frac{0.2\:\text{m}}{6\:\text{m/s}} = (1)/(30)\:\text{s}`

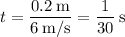
The fastest speed that the wheel can spin without clipping the arrow is

`v = (s)/(t) = \frac{0.196\:\text{m}}{\left(\frac{1}{30\:\text{s}}\right)} = 5.9\:\text{m/s}`

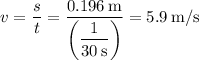
The angular velocity
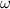`\omega` of the wheel is given by

`\omega = (v)/(r) = \frac{5.9\:\text{m/s}}{0.25\:\text{m}} = 23.6\:\text{rad/s}`

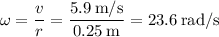
In terms of rev/s, we can convert the answer above as follows:

`23.6\:\frac{\text{rad}}{\text{s}}×\frac{1\:\text{rev}}{2\pi\:\text{rad}} = 3.8\:\text{rev/s}`

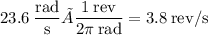
As you probably noticed, I did the calculations based on the assumption that I'm aiming for the edge of the wheel because this is the part of the wheel where a point travels a longer linear distance compared to ones closer to the axle, thus giving the arrow a better chance to pass through the wheel without getting clipped by the spokes. If you aim closer to the axle, then the wheel needs to spin slower to allow the arrow to get through without hitting the spokes.