Answer:
D) 54 cm
Explanation:
We can use the Centroid Theorem to solve this problem, which states that the centroid of a triangle is
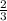 of the distance from each of the triangle's vertices to the midpoint of the opposite side.
of the distance from each of the triangle's vertices to the midpoint of the opposite side.
Therefore,
 is
is
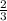 of the distance from
of the distance from
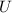 to
to
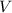 , since the latter is the midpoint of the side opposite to
, since the latter is the midpoint of the side opposite to
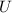 . We know this because
. We know this because
 belongs to
belongs to
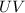 , so
, so
 must be
must be
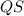 's midpoint due to the fact that by definition, the centroid of a triangle is the intersection of a triangle's three medians (segments which connect a vertex of a triangle to the midpoint of the side opposite to it).
's midpoint due to the fact that by definition, the centroid of a triangle is the intersection of a triangle's three medians (segments which connect a vertex of a triangle to the midpoint of the side opposite to it).
We can then write the following equation:
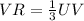
Substituting
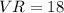 into the equation gives us:
into the equation gives us:
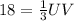
Solving for
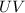 , we get:
, we get:
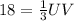
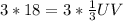 (Multiply both sides of the equation by
(Multiply both sides of the equation by
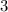 to get rid of
to get rid of
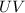 's coefficient)
's coefficient)
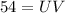 (Simplify)
(Simplify)
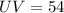 (Symmetric Property of Equality)
(Symmetric Property of Equality)
Therefore, the answer is D. Hope this helps!