Question

The graph of y = 4x2 - 4x – 1 is shown.

Use the graph to find estimates for
the solutions of
i) 4x2 - 4x – 1 = 0
ii) 4x2 - 4x - 1 = 2

Answer 1

i) The approximate solutions are:
`x_(1) \approx -0.207`,
`x_(2) \approx 1.207`.

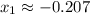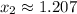ii) The approximate solutions are:
`x_(1)\approx -0.5`,
`x_(2) \approx 1.5`.

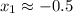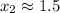Explanation:

i) The best approach to estimate graphically the solution of
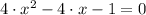`4\cdot x^(2) - 4\cdot x - 1 = 0` is graphing the following system of equations:

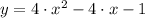`y = 4\cdot x^(2)-4\cdot x - 1` (1)

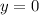`y = 0` (2)

And labeling the points in which both intersects each other. We include the result in the image 'solution-i'. The approximate solutions are:
`x_(1) \approx -0.207`,
`x_(2) \approx 1.207`.

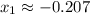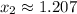ii) The best approach to estimate graphically the solution of
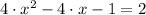`4\cdot x^(2) - 4\cdot x - 1 = 2` is graphing the following system of equations:

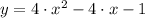`y = 4\cdot x^(2)-4\cdot x - 1` (1)

`y = 2` (2)

And labeling the points in which both intersects each other. We include the result in the image 'solution-ii'. The approximate solutions are:
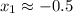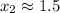`x_(1)\approx -0.5`,
`x_(2) \approx 1.5`.