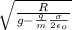Answer:
a)
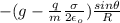 =
=
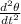
b) f = 2π
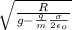
Step-by-step explanation:
a) To have the equations of motion, let's use Newton's second law.
Let's set a reference system where the x-axis is parallel to the path and the y-axis is in the direction of tension of the rope.
For this reference system the tension is in the direction of the y axis, we must decompose the weight and the electrical force.
Let's use trigonometry for the weight that is in the vertical direction down
sin θ = Wₓ / W
cos θ = W_y / w
Wₓ = W sin θ
W_y = W cos θ
we repeat for the electric force that is vertical upwards
F_{ex} = F_e sin θ
F_{ey} = F_e cos θ
the electric force is
F_e = q E
where the field created by an infinite plate is
E =
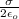
let's write Newton's second law
Y axis
T - W_y = 0
T = W cos θ
X axis
F_{ex} - Wₓ = m a (1)
we use that the acceleration is related to the position
a = dv / dt
v = dx / dt
where x is the displacement in the arc of the curve
substituting
a = d² x /dt²
we substitute in 1
q E sin θ - mg sin θ = m
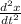
we have angular (tea) and linear (x) variables, if we remember that angles must be measured in radians
θ = x / R
x = R θ
we substitute
sin θ (q E - mg) = m \frac{d^2 R \ theta}{dt^2}
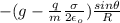 =
=
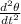
this is the equation of motion of the system
b) for small oscillations
sin θ = θ
therefore the solution is simple harmonic
θ = θ₀ cos (wt + Ф)
if derived twice, we substitute
- ( g - \frac{q}{m} \frac{\sigma }{ 2 \epsilon_o} ) \frac{\theta}{R } θ₀ cos (wt + Ф) = -w² θ₀ cos (wt + Ф)
w² =
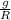 -
-
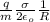
angular velocity is related to frequency
w = 2π f
f = 2π / w
f = 2π/w
f = 2π