Given:
The vertex of a quadratic function is (4,-7).
To find:
The equation of the quadratic function.
Solution:
The vertex form of a quadratic function is:
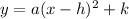 ...(i)
...(i)
Where a is a constant and (h,k) is vertex.
The vertex is at point (4,-7).
Putting h=4 and k=-7 in (i), we get
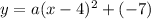
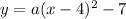
The required equation of the quadratic function is
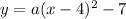 where, a is a constant.
where, a is a constant.
Putting a=1, we get

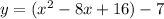
![[\because (a-b)^2=a^2-2ab+b^2]](https://img.qammunity.org/2022/formulas/mathematics/college/5g4f7w0d9ahy69ly1oxw8vqo5n8zn5stjf.png)
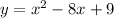
Therefore, the required quadratic function is
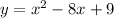 .
.