Given:
The system of equation is
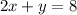
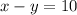
To find:
The value of the system determinant.
Solution:
If two equations of a system of equations are
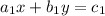 and
and
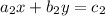 , then the system determinant is
, then the system determinant is
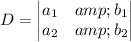
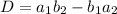
The given two equations are
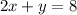 and
and
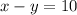 .
.
Here,
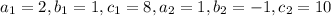 .
.
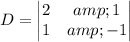
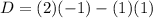

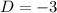
The value of the system determinant is -3. Therefore, the correct option is C.