Question

PLEASE ANSWER WILL GIVE POINTS!!!!!!!!!!!

Answer 1

Given:

The figure of a right triangle ABC.

To find:

The trigonometric ratios
`\sin B, \tan A, \cos B`.

Solution:

Using Pythagoras theorem,

`Hypotenuse^2=Perpendicular^2+Base^2`

`AB^2=AC^2+BC^2`

`(10)^2=(6)^2+BC^2`

`100-36=BC^2`

`64=BC^2`

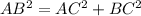
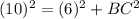
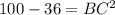
Taking square root on both sides.

`√(64)=BC`

`8=BC`

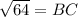
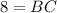
So, measure of BC is 8 units.

Now,

`\sin \theta=(Opposite)/(Hypotenuse)`

`\sin B=(AC)/(AB)`

`\sin B=(6)/(10)`

`\sin B=(3)/(5)`

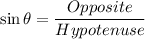
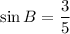
Similarly,

`\tan \theta=(Opposite)/(Adjacent)`

`\tan A=(AC)/(BC)`

`\tan A=(6)/(8)`

`\tan A=(3)/(4)`

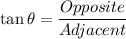
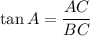
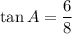
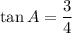
And,

`\cos \theta=(Adjacent)/(Hypotenuse)`

`\cos B=(BC)/(AB)`

`\cos B=(8)/(10)`

`\cos B=(4)/(5)`

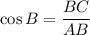
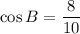
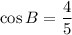
Therefore, the required trigonometric ration are
`\sin B=(3)/(5), \tan A=(3)/(4), \cos B=(4)/(5)`.