Answer:

Explanation:
Start multiplying and adding all together. You get
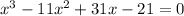 .
.
At this point we're stuck factoring since there exist a formula for the roots, but it's nowhere easy to remember. We start writing down The List (rational root theorem: it's the divisor of the constant term divided by the divisor of the lead coefficent, with a plus or minus, in our case it's
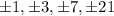 ) and let's try checking one by one.
) and let's try checking one by one.
Value
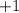 gives a zero on the LHS, it means the polynomial is divisible by
gives a zero on the LHS, it means the polynomial is divisible by
 . By doing the division, or writing it as
. By doing the division, or writing it as
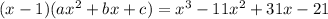 , multiplying on the LHS and then finding the values of a, b, and c (easiest for me, your mileage may vary) we can write our expression, finally, as
, multiplying on the LHS and then finding the values of a, b, and c (easiest for me, your mileage may vary) we can write our expression, finally, as
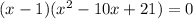 At this point you can either apply the quadratic formula or decompose again the second factor as
At this point you can either apply the quadratic formula or decompose again the second factor as
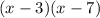 by finding two numbers whose sum is -10 and product is 21, ie -3 and -7. At this point the expression
by finding two numbers whose sum is -10 and product is 21, ie -3 and -7. At this point the expression
 is true if
is true if
