Question

Use the figure below to solve for the value of x.

Answer 1

Given:

A figure of a right triangle and an altitude form the right angle vertex to hypotenuse.

To find:

The value of x.

Solution:

From the given figure, it is clear that the altitude divides the hypotenuse in two segments x and 8.

Length of altitude = 18

If an altitude divide the hypotenuse in 2 segments, then according to the geometric mean theorem, the length of the altitude is the geometric mean of two segments of hypotenuse.

By using geometric mean theorem, we get

`18=√(x* 8)`
`[\because \text{Geometric mean of }a,b,c:b=√(ac)]`

`18^2=8x`

`324=8x`

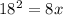
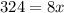
Divide both sides by 8.

`(324)/(8)=x`

`40.5=x`

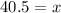
Therefore, the value of x is 40.5.