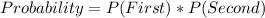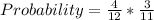Question

marbles numbered from 1 to 12 are put in a bag. if marbles are not put back into the bag after being drawn, what is the probability of drawing two prime numbers in a row?

Answer 1

`Probability = (1)/(11)`

Explanation:

Given

Marbles = 12

Selection without replacement

Required

Determine the probability of selecting 2 primes

Between 1 and 12, the prime digits is 4, and they are: 3, 5, 7 and 11

So, when the first marble is picked, the probability that it will be prime is:

`P(First) = (4)/(12)`

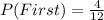
Now there are 3 primes left and 11 marbles in total. So, the probability of selecting another prime is:

`P(Second) = (3)/(11)`

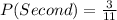
The required probability is:

`Probability = P(First) * P(Second)`

`Probability = (4)/(12) * (3)/(11)`

`Probability = (1)/(11)`