Question

Simplify
`x^(2) - 36`

Answer 1

`(x-6)(x+6)`

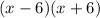
Explanation:

In order to simplify this equation, one must use the quadratic factoring patterns. These patterns are as follows:

`a^2-b^2=(a-b)(a+b)`

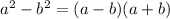
This pattern works because, if one is to distribute the terms in the parenthesis by multiplying each term in one of the parenthesis by every term in the other, the result is the original equation:

`(a-b)(a+b)\\\\=(a)(a)+(a)(-b)+(a)(b)+(b)(-b)\\\\=a^2-ab+ab-b^2\\\\=a^2-b^2`

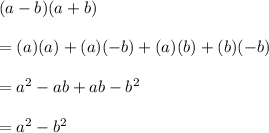
One can apply this pattern to the given equation, remember (6) times itself equals (36). Therefore, one can state the following: (
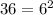`36=6^2`), thus one can apply it to the given equation:

`x^2-36\\\\=x^2-6^2\\\\=(x-6)(x+6)`

Answer 2

`{x}^(2) - 36 \\ = (x + 6)(x - 6)`

Explanation:

x^2-36

(x+6) ( x-6)

it's helpful to you