Answer:
see explanation
Explanation:
Since QR is a perpendicular bisector then Δ RST is isosceles
with 2 congruent legs , that is
RT = RS , substitute values
6x - 4 = 3x + 8 ( subtract 3x from both sides )
3x - 4 = 8 ( add 4 to both sides )
3x = 12 ( divide both sides by 3 )
x = 4
Then RS = 3x + 8 = 3(4) + 8 = 12 + 8 = 20
so RT = RS = 20
Using Pythagoras' identity in right triangle QRT
QT² + QR² = RS²
QT² + 12² = 20²
QT² + 144 = 400 ( subtract 144 from both sides )
QT² = 256 ( take square root of both sides )
QT =
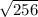 = 16
= 16
In summary
RS = 12 is False ( RS = 20 )
x = 4 is True
x = 3 is False
QT = 16 is True