Question

You walk 100m due north. You then turn and walk 55m due east. You then make another turn and walk 12m due south. What is the resultant vector for your walk?

Answer 1

Step-by-step explanation:

Important here is to know that due north is a 90 degree angle, due east is a 0 degree angle, and due south is a 270 degree angle. Then we find the x and y components of each part of this journey using the sin and cos of the angles multiplied by each magnitude:

`A_x=100cos90\\A_x=0\\B_x=55cos0\\B_x=55\\C_x=12cos270\\C_x=55`

Add them all together to get the x component of the resultant vector, V:

`V_x=55`

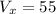
Do the same to find the y components of the part of this journey:

`A_y=100sin90\\A_y=100\\B_y=55sin0\\B_y=0\\C_y=12sin270\\C_y=-12`

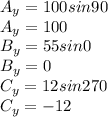
Add them together to get the y component of the resultant vector, V:

`V_y=88`

One thing of import to note is that both of these components are positive, so the resultant angle lies in QI.

We find the final magnitude:

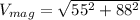`V_(mag)=√(55^2+88^2)` and, rounding to 2 sig dig's as needed:

`V_(mag)=` 1.0 × 10² m; now for the direction:

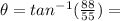`\theta=tan^(-1)((88)/(55))=` 58°