Solution :
The test is distributed normally with mean of 72.8 and the standard deviation of 7.3
Finding numerical limits for the D grade.
D grade : Scores below the top 80% and above the bottom 10%.
Let the bottom limit for D grade be
 and the top limit for D grade be
and the top limit for D grade be
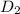 .
.
First find the bottom numerical limit for a D grade is :

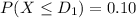
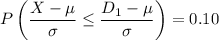
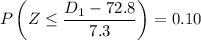 ..........(1)
..........(1)
From (1)

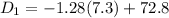
= 63.45
≈ 64
Now the top numerical limit for D grade :
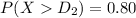
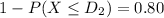
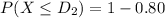
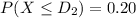

 ..........(2)
..........(2)
From (2)
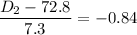
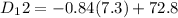
= 66.668
≈ 67
Therefore, the numerical limit for a D grade is 64 to 67.