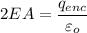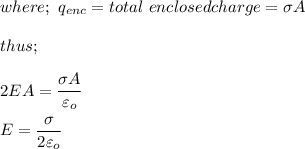Answer:
Step-by-step explanation:
Consider an endless sheet of uniform charge thickness per unit area

For a boundless sheet of charge, the electric field will be opposite to the surface. In this way, just the closures of a round and hollow Gaussian surface will add to the electric transition. For this situation, around and hollow Gaussian surface opposite to the charge sheet is utilized. The subsequent field is a large portion of that of a conductor at harmony with this surface charge thickness.
By balance, we expect the electric field on one or the other side of a plane to be an element of x just to be guided typical to the plane and to point away from/towards the plane contingent upon whether,
 is positive/negative.
is positive/negative.
According to the law;