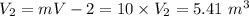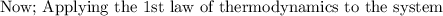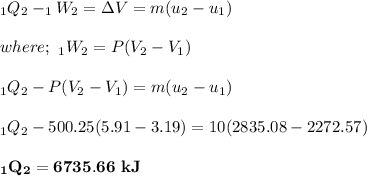Question

A vertical piston cylinder assembly contains 10.0kg of a saturated liquid-vapor water mixture with initial quality of 0.85 The water receives energy by heat transfer until the temperature reaches 320*C. The piston has a mass of 204kg and area of 0.005m2. Atmospheric pressure of 100kPa acts on the top side of the piston. Local gravitational acceleration is 9.81m/s2 Calculate the amount of heat transfer between the water and the surroundings in kJ. Enter a numeric value only. 6735.66

Answer 1

Step-by-step explanation:

From the given information:

At state 1:

Initial Quality
`= x_1 = 0.85`

mass = 10.0 kg

At state 2:

Temperature
`T_2 = 320^0`

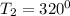
mass of the piston
`m_p = 204 \ kg`

area of the piston
`A_p = 0.00 5 \ m^2`

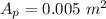
Atmospheric pressure
`P_(atm)= 100 \ kPa = 100 * 10^3 \ Pa`

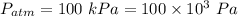
Gravitational acceleration = 9.81 m/s²

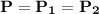`\mathbf{P= P_1=P_2}`, This is because there exists no restriction to the movement of the piston and provided the process is frictionless. So, the process 1-2 is regarded as constant.

To calculate the applying force balance over the piston by using force balance in the vertical direction:

`\mathbf{P_(AP) = P_(atmA_p) + m_pg}`

∴

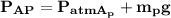
(100 × 10³)×0.005 + 204 × 9.31 = P × 0.05

P = 500248 Pa

P = 500.25 kPa

At state 1:

`\mathbf{P_1 = P = 500.25 \ kPa}`

`x_1 = 0.85`

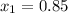
Hence, this is a saturated mixture of liquid and vapor

Using the steam tables at 500.25 kPa

`V_f = 1.093 * 10^(-3) \ m^3/kg \\ \\ V_g = 0.375 \ m^3/kg \\ \\ U_f = 639.72 \ kJ/kg \\ \\ U_g = 2560.72 \ kJ/kg`

∴

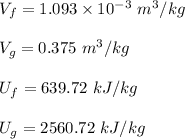
Specific volume at state 1 is given as:

`V_1 = [ V_f +x_1(v_g -v_f) ] \ at \ 500.25 \ kPa \\ \\ V_1 = 0.319 \ m^3/kg`

volume at state 1 is given by:

`V_1 = mV_1 = 10 * 0.319 \\ \\ V_1 = 3.19 \ m^3`

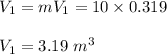
Similarly, the specific internal energy is:

`U_1 = [U_f +x_1 (U_o-Uf)] \ at \ 500.25 \ kPa`

`U_1 = 639.72 +0.82 (2560.72 -639.72)`

`U_1 = 2272.57 \ kJ/kg`

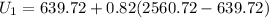
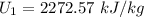
At state 2:

`P = P_1 = P_2 = 500.25 \ kPa \\ \\ T_2 = 320^0 \ C`

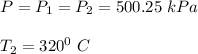
Using steam tables at P = 500.25 kPa and T = 320° C

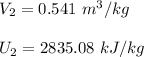
`V_2 = 0.541 \ m^3/kg \\ \\ U_2 = 2835.08 \ kJ/kg`

∴

`V_2 = mV-2 = 10 * V_2 = 5.41 \ m^3`

`\text{Now; Applying the 1st law of thermodynamics to the system}`

`_1Q_2 -_1W_2 = \Delta V =m(u_2-u_1) \\ \\ where;\ _1W_2 = P(V_2-V_1) \\ \\ _1Q_2 -P(V_2-V_1) = m(u_2-u_1) \\ \\ _1Q_2 - 500.25(5.91 -3.19) = 10( 2835.08 -2272.57) \\ \\ \mathbf{ _1Q_2 = 6735.66 \ kJ}`