1 Answer

Mechnicov · Answer 1 · 2023-10-22T09:13:44+0000

Explanation:

Let x represent the first number, and y be the second number.

The first statement can be modeled as

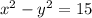
${x}^(2) - {y}^(2) = 15$

The second statement can modeled as

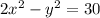
$2 {x}^(2) - {y}^(2) = 30$

If we multiply 2 both sides of the first equation,

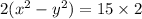
$2( {x}^(2) - {y}^(2) ) = 15 * 2$

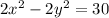
$2 {x}^(2) - 2 {y}^(2) = 30$

Subsitue this for 30 in second equation,

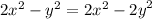
$2 {x}^(2) - {y}^(2) = 2 {x}^(2) - {2y}^(2)$

${y}^(2) = 0$

y = 0

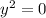
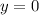
Subsitue this for y in either equation,

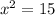${x}^(2) = 15$ So our answer is

plus or minus sqr root of 15, 0).

(± √(15) ,0)

x = √(15)

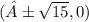
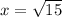
or

x = - √(15)

Please log in or register to add a comment.