Question

State a cubic or quartic function with the least degree possible in intercept form for the given graph. Assume that all x-intercepts are integers, and that the constant factor a is either 1 or −1.

Enter the correct value in the box to answer the question.
y= ?

Answer 1

y =
`-x^(3) - 2x^(2) + 5x + 6`

Explanation:

The function will be cubic. The x-intercepts are -4, -1, and 2

The constant factor is -1 because the graph falls on the right. So,

y = -(x + 4)(x + 1)(x - 2)

y = -
`x^(3) -2x^(2) + 5x +6`

Answer 2

y =
`-x^3-2x^2+5x+6`

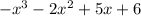
To construct a cubic function in intercept form with integer x-intercepts and a constant factor a of either 1 or -1, we consider the properties of intercepts and the general form of cubic functions. The intercept form of a cubic function is given by y=a(x−r1)(x−r2)(x−r3), where r1, r2 and r3 are the x-intercepts.

To maintain simplicity and meet the specified conditions, we choose a=1 and opt for three distinct integer roots (r1, r2 and r3).

The function will be cubic. The x-intercepts are -4, -1, and 2

The constant factor is -1 because the graph falls on the right. So,

y = -(x + 4)(x + 1)(x - 2)

y=-x^3-2x^2+5x+6