Question

A digital communication channel transmits bits of information, usually designated as 0 and 1. If a sender transmits a 0, he/she hopes the recipient receives a 0. If a sender transmits a 1, he/she hopes that the recipient receives a 1. Unfortunately, this is not always the case. Suppose on a certain transmission line, a transmitted 0 is received correctly 90% of the time (10% of the time a 1 is received), and a transmitted 1 is received correctly 74% of the time. (26% of the time a 0 is received.) It is known that on this transmission line, 80% of all bits transmitted are 0 bits. A randomly selected transmitted bit is examined. Say its value is X. The bit received is Y. a.What is the probability that X

Answer 1

a) 0.80

b) 0.72

c) 0.02

Explanation:

It is assumed that

X = Bit transmitted

Y = Bit received

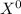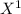`X^(0)` = Transmissted bit is 0

`X^(1)` = Transmissted bit is 1

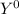`Y^(0)` = Received bit is 0

`Y^(1)` = Received bit is 1

As per the given condition

P [
`Y^(0)` |
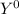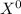`X^(0)` ] = 90%

P [
`Y^(0)` |
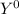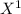`X^(1)` ] = 100% - 90% = 10%

P [
`Y^(1)` |
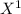`X^(1)` ] = 74%

P [
`Y^(0)` |
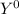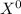`X^(0)` ] = 100% - 74% = 26%

P [ Tramitted bits are 0 ] = 80%

Now calculate each situation

a)

As all the transmitted bits are o has possibilit of 80% then

P [ X = 0 ] = P [
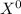`X^(0)` ] = 80% = 0.80

b)

P [ X = 0, Y = 0 ] = P [
`X^(0)` ,
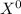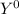`Y^(0)` ] = P [
`Y^(0)` |
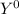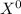`X^(0)` ] x P [
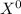`X^(0)` ] = 90% x 80% = 72% = 0.72

c)

P [ X = 1, Y = 0 ] = P [
`X^(1)` ,
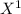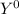`Y^(0)` ] = P [
`Y^(0)` |
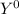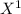`X^(1)` ] x P [
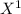`X^(1)` ] = 10% x ( 100% - 80% ) = 10% x 20% = 2% = 0.02