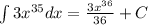Question

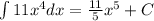
Find the indefinite integrals, if possible, using the formulas and techniques you have studied so far in the text.(a) 11 x4 dxThis integral can be evaluated using the basic integration rules.This integral cannot be evaluated using the basic integration rules. (b) 8x1 x4 dxThis integral can be evaluated using the basic integration rules.This integral cannot be evaluated using the basic integration rules. (c) 3x31 x4 dxThis integral can be evaluated using the basic integration rules.This integral cannot be evaluated using the basic integration rule

Answer 1

a) This integral can be evaluated using the basic integration rules.
`\int 11x^(4)dx = (11)/(5) x^(5)+C`

b) This integral can be evaluated using the basic integration rules.
`\int 8x^(1)x^(4)dx=(4)/(3)x^(6)+C`

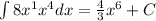
c) This integral can be evaluated using the basic integration rules.
`\int 3x^(31)x^(4)dx=(x^(36))/(12)+C`

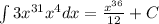
Explanation:

a)
`\int 11x^(4)dx`

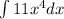
In order to solve this problem, we can directly make use of the power rule of integration, which looks like this:

`\int kx^(n)=k(x^(n+1))/(n+1)+C`

so in this case we would get:

`\int 11x^(4)dx=11 (x^(4+1))/(4+1)+C`

`\int 11x^(4)dx=11 (x^(5))/(5)+C`

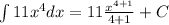
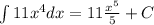
b)
`\int 8x^(1)x^(4)dx`

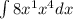
In order to solve this problem we just need to use some algebra to simplify it. By using power rules, we get that:

`\int 8x^(1)x^(4)dx=\int 8x^(1+4)dx=\int 8x^(5)dx`

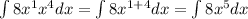
So we can now use the power rule of integration:

`\int 8x^(5)dx=(8)/(5+1)x^(5+1)+C`

`\int 8x^(5)dx=(8)/(6)x^(6)+C`

`\int 8x^(5)dx=(4)/(3)x^(6)+C`

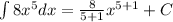
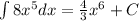
c) The same applies to this problem:

`\int 3x^(31)x^(4)dx=\int 3x^(31+4)dx=\int 3x^(35)dx`

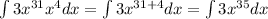
and now we can use the power rule of integration:

`\int 3x^(35)dx=(3x^(35+1))/(35+1)+C`

`\int 3x^(35)dx=(3x^(36))/(36)+C`

`\int 3x^(35)dx=(x^(36))/(12)+C`