Question

asked May 6, 2022 143k views

1 Answer

Herrmarek · Answer 1 · 2022-05-12T19:36:55+0000

Answer:

0.207 = 20.7% probability that the wait time will be more than an additional 41 minutes

Explanation:

To solve this question, we should understand the exponential distribution and conditional probability.

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

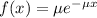
$f(x) = \mu e^(-\mu x)$

In which
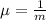$\mu = (1)/(m)$ is the decay parameter.

The probability that x is lower or equal to a is given by:

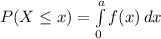
$P(X \leq x) = \int\limits^a_0 {f(x)} \, dx$

Which has the following solution:

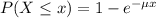
$P(X \leq x) = 1 - e^(-\mu x)$

The probability of finding a value higher than x is:

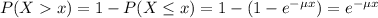
$P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^(-\mu x)) = e^(-\mu x)$

Conditional Probability

We use the conditional probability formula to solve this question. It is

$P(B|A) = (P(A \cap B))/(P(A))$

In which

P(B|A) is the probability of event B happening, given that A happened.

$P(A \cap B)$ is the probability of both A and B happening.

P(A) is the probability of A happening.

The average waiting time for this distribution is 38 minutes.

This means that
$m = 38, \mu = (1)/(38) = 0.0263$

Given that it has already taken 37 minutes, what is the probability that the wait time will be more than an additional 41 minutes?

Event A: Taking more than 37 minutes.

Event B: More than 37 + 41 = 78 minutes.

Probability of taking more than 37 minutes:

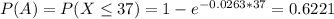
$P(A) = P(X \leq 37) = 1 - e^(-0.0263*37) = 0.6221$

More than 37 minutes and more than 78 minutes:

The intersection is more than 78 minutes, so:

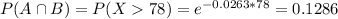
$P(A \cap B) = P(X > 78) = e^(-0.0263*78) = 0.1286$

The probability is:

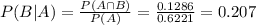
$P(B|A) = (P(A \cap B))/(P(A)) = (0.1286)/(0.6221) = 0.207$

0.207 = 20.7% probability that the wait time will be more than an additional 41 minutes

Please log in or register to add a comment.