Answer:
See below
Explanation:
we want to prove that A.M, G.M. and H.M between any two unequal positive numbers satisfy the following relations.
- (G.M)²= (A.M)×(H.M)
- A.M>G.M>H.M
well, to do so let the two unequal positive numbers be
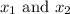 where:
where:
the AM,GM and HM of
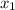 and
and
 is given by the following table:
is given by the following table:
![\begin{array} \hline AM& GM& HM\\ \hline (x_(1) + x_(2))/(2) & \sqrt{x_(1) x_(2)} & (2)/( (1)/(x_(1) ) + (1)/(x_(2)) ) \\ \hline\end{array}]()
Proof of I:
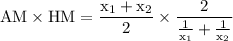
simplify addition:

reduce fraction:
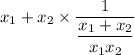
simplify complex fraction:
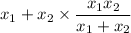
reduce fraction:
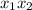
rewrite:
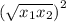

hence, PROVEN
Proof of II:

square root both sides:
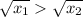
isolate right hand side expression to left hand side and change its sign:

square both sides:
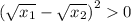
expand using (a-b)²=a²-2ab+b²:

move -2√x_1√x_2 to right hand side and change its sign:
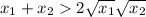
divide both sides by 2:
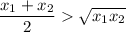

again,
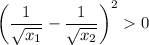
expand:

move the middle expression to right hand side and change its sign:


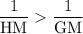
cross multiplication:

hence,
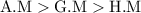
PROVEN