Question

Prove that A.M, G.M. and H.M between any two unequal positive numbers satisfy the following relations.

i. (G.M)²= (A.M)×(H.M)
ii.A.M>G.M>H.M​

Answer 1

See below

Explanation:

we want to prove that A.M, G.M. and H.M between any two unequal positive numbers satisfy the following relations.

1. (G.M)²= (A.M)×(H.M)
2. A.M>G.M>H.M

well, to do so let the two unequal positive numbers be
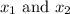`\text{$x_1$ and $x_2$}` where:

• 
  `x_(1) > x_(2)`

the AM,GM and HM of
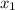`x_1` and
`x_2` is given by the following table:

Proof of I:

`\displaystyle \rm AM * HM = (x_(1) + x_(2))/(2) * (2)/( (1)/(x_(1) ) + (1)/(x_(2)) )`

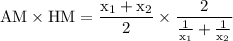
simplify addition:

`\displaystyle (x_(1) + x_(2))/(2) * (2)/( (x_(1) + x_(2))/(x_(1) x_(2)) )`

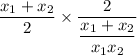
reduce fraction:

`\displaystyle x_(1) + x_(2) * (1)/( (x_(1) + x_(2))/(x_(1) x_(2)) )`

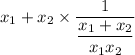
simplify complex fraction:

`\displaystyle x_(1) + x_(2) * (x_(1) x_(2))/(x_(1) + x_(2))`

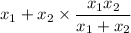
reduce fraction:

`\displaystyle x_(1) x_(2)`

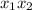
rewrite:

`\displaystyle (\sqrt{x_(1) x_(2)} {)}^(2)`

`\displaystyle AM * HM = (GM{)}^(2)`

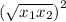
hence, PROVEN

Proof of II:

`\displaystyle x_(1) > x_(2)`

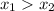
square root both sides:

`\displaystyle \sqrt{x_(1) }> \sqrt{ x_(2)}`

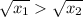
isolate right hand side expression to left hand side and change its sign:

`\displaystyle\sqrt{x_(1) } - \sqrt{ x_(2)} > 0`

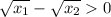
square both sides:

`\displaystyle(\sqrt{x_(1) } - \sqrt{ x_(2)} {)}^(2) > 0`

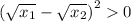
expand using (a-b)²=a²-2ab+b²:

`\displaystyle x_(1) -2\sqrt{x_(1) }\sqrt{ x_(2)} + x_(2) > 0`

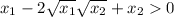
move -2√x_1√x_2 to right hand side and change its sign:

`\displaystyle x_(1) + x_(2) > 2 \sqrt{x_(1) } \sqrt{ x_(2)}`

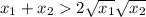
divide both sides by 2:

`\displaystyle (x_(1) + x_(2))/(2) > \sqrt{x_(1) x_(2)}`

`\displaystyle \boxed{ AM>GM}`

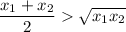
again,

`\displaystyle \bigg( \frac{1}{\sqrt{x_(1) }} - \frac{1}{\sqrt{ x_(2)}} { \bigg)}^(2) > 0`

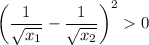
expand:

`\displaystyle (1)/(x_(1)) - \frac{2}{\sqrt{x_(1) x_(2)} } + (1)/(x_(2) )> 0`

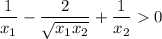
move the middle expression to right hand side and change its sign:

`\displaystyle (1)/(x_(1)) + (1)/(x_(2) )> \frac{2}{\sqrt{x_(1) x_(2)} }`

`\displaystyle ((1)/(x_(1)) + (1)/(x_(2) ))/(2)> \frac{1}{\sqrt{x_(1) x_(2)} }`

`\displaystyle \rm (1)/( HM) > (1)/(GM)`

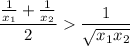
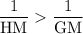
cross multiplication:

`\displaystyle \rm \boxed{ GM >HM}`

hence,

`\displaystyle \rm A.M>G.M>H.M`

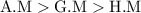
PROVEN