Question

In Exercises 45–48, let f(x) = (x - 2)2 + 1. Match the
function with its graph

Answer 1

45) The function corresponds to graph A

46) The function corresponds to graph C

47) The function corresponds to graph B

48) The function corresponds to graph D

Explanation:

We know that the function f(x) is:

`f(x)=(x-2)^(2)+1`

45)

The function g(x) is given by:

`g(x)=f(x-1)`

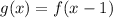
using f(x) we can find f(x-1)

`g(x)=((x-1)-2)^(2)+1=(x-3)^(2)+1`

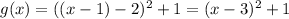
If we take the derivative and equal to zero we will find the minimum value of the parabolla (x,y) and then find the correct graph.

`g(x)'=2(x-3)`

`2(x-3)=0`

`x=3`

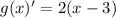
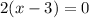
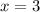
Puting it on g(x) we will get y value.

`y=g(3)=(3-3)^(2)+1`

`y=g(3)=1`

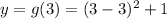
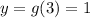
Then, the minimum point of this function is (3,1) and it corresponds to (A)

46)

Let's use the same method here.

`g(x)=f(x+2)`

`g(x)=((x+2)-2)^(2)+1`

`g(x)=(x)^(2)+1`

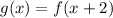
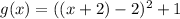
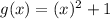
Let's find the first derivative and equal to zero to find x and y minimum value.

`g'(x)=2x`

`0=2x`

`x=0`

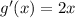
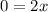
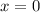
Evaluatinf g(x) at this value of x we have:

`g(0)=(x)^(2)+1`

`g(0)=1`

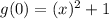
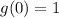
Then, the minimum point of this function is (0,1) and it corresponds to (C)

47)

Let's use the same method here.

`g(x)=f(x)+2`

`g(x)=(x-2)^(2)+1+2`

`g(x)=(x-2)^(2)+3`

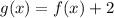
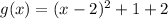
Let's find the first derivative and equal to zero to find x and y minimum value.

`g'(x)=2(x-2)`

`0=2(x-2)`

`x=2`

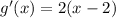
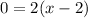
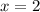
Evaluatinf g(x) at this value of x we have:

`g(2)=(2-2)^(2)+3`

`g(2)=3`

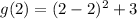
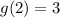
Then, the minimum point of this function is (2,3) and it corresponds to (B)

48)

Let's use the same method here.

`g(x)=f(x)-3`

`g(x)=(x-2)^(2)+1-3`

`g(x)=(x-2)^(2)-2`

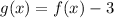
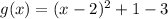
Let's find the first derivative and equal to zero to find x and y minimum value.

`g'(x)=2(x-2)`

`0=2(x-2)`

`x=2`

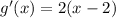
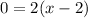
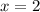
Evaluatinf g(x) at this value of x we have:

`g(2)=(2-2)^(2)-2`

`g(2)=-2`

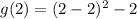
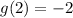
Then, the minimum point of this function is (2,-2) and it corresponds to (D)

I hope it helps you!